Bitcoin is al vijf keer gestorven en ten grave gedragen. Het speelkwartier is voorbij, vanaf nu is het beursplein weer voor de grote mensen die handelen en investeren in echte assets. Of toch niet?
Samenvatting
- Bitcoin wordt bij elke daling van meer dan 30 procent wel ergens dood verklaard. Vaak onderbouwd met een lineaire grafiek.
- De adoptie van bitcoin verloopt exponentieel, en de groei van de koers (dus) ook. Daarbij past een logaritmische grafiek. En dan zie je dat het allemaal reuze meevalt.
Vandaag gaan we het hebben over de y-as van bitcoinkaarten. De meeste grafieken die je ziet van bijvoorbeeld aandelen, grondstoffen en rentestanden zijn lineaire grafieken. Dat betekent dat elk streepje op de as een optelling is: 1, 2, 3, 4, 5, enzovoorts.
Dat is logisch omdat vraag en aanbod normaal gesproken in een volwassen markt een lineair verschijnsel zijn, en de groei en krimp van de waarde van een asset of een markt dus ook. Er zijn ook wel exponentiële invloeden, zoals bevolkingsgroei en inflatie, maar die zijn zo klein dat ze de grafiek nauwelijks vertekenen.
Hieronder zie je de grafiek van de zilverprijs in dollars van de afgelopen vijftien jaar. De afstand tussen de streepjes op de y-as is telkens 5 dollar. Een uitstekend bruikbare grafiek.
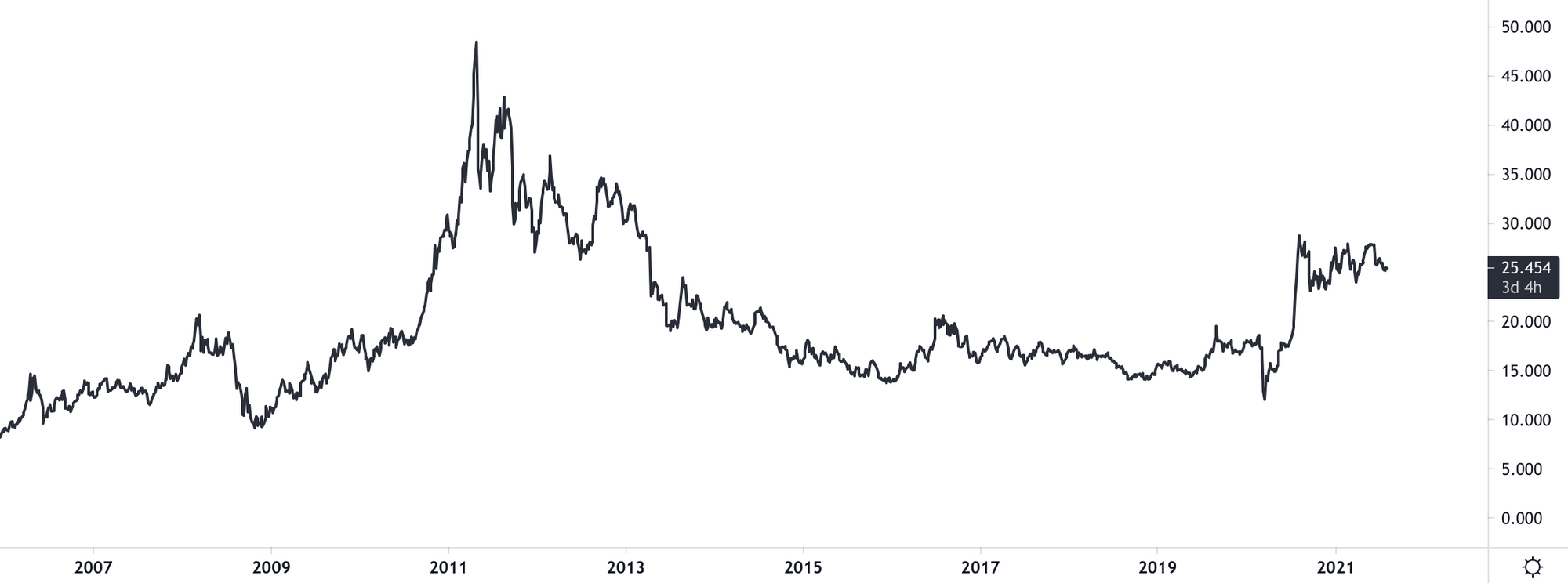
Laten we nu eens naar de bitcoingrafiek kijken op een lineaire schaal. Dit is de bitcoinkoers tot en met vorige week toen de koers iets onder de 30.000 dollar stond. Dat moment heb ik even gekozen voor het dramatische effect. Dit ziet er namelijk niet erg rooskleurig uit, of wel? Gizmodo schreef: “Bitcoin is headed for zero”.

Mensen die al wat langer naar bitcoinkaarten kijken, hebben zoiets vaker gezien. Ik heb de data even teruggespoeld naar begin 2018. Laten we eens kijken hoe dat eruit ziet. Forbes schreef toen: “Is Bitcoin Going To Zero?”
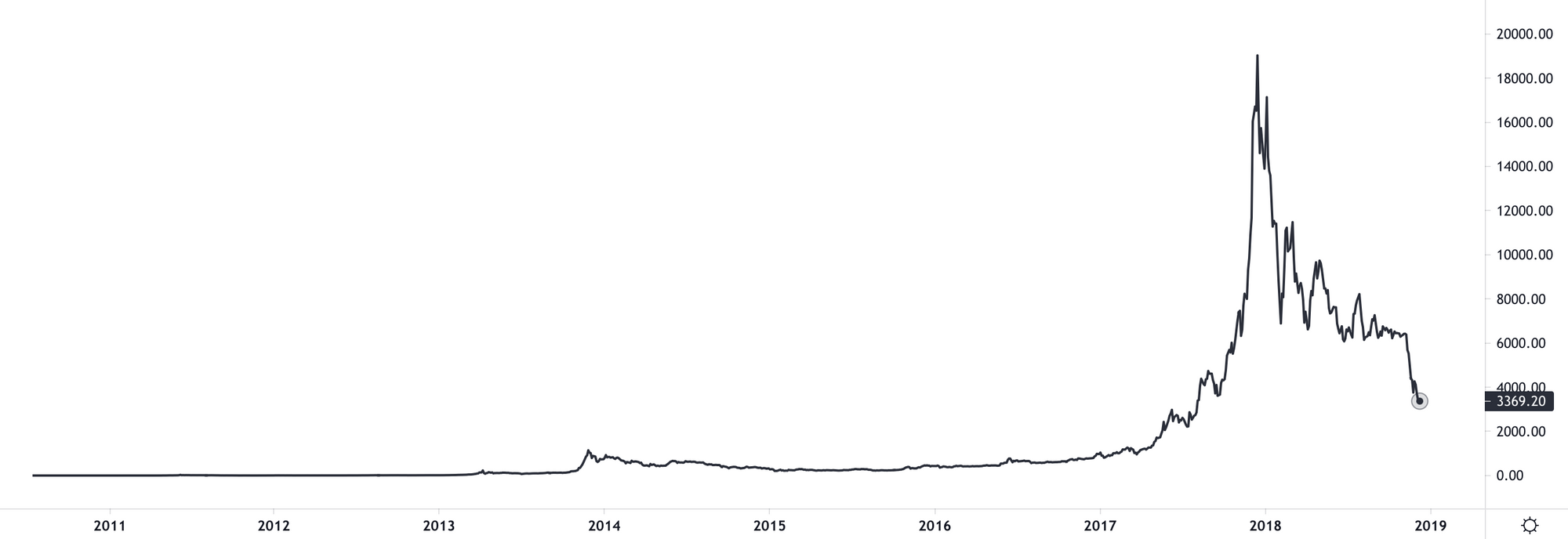
Laten we nog wat verder in de geschiedenis kijken, want hoewel het links van 2018 tamelijk vlak lijkt, verandert dit als je alles na 2017 eraf knipt. Zo zag het eruit begin 2015. Fortune kopte toen: “Bitcoin will not survive”

Okay, punt gemaakt Bert! Nee, zo makkelijk kom je niet van me af. Hier de kaart in 2013. Bloomberg merkte op: “Bitcoin is still doomed”
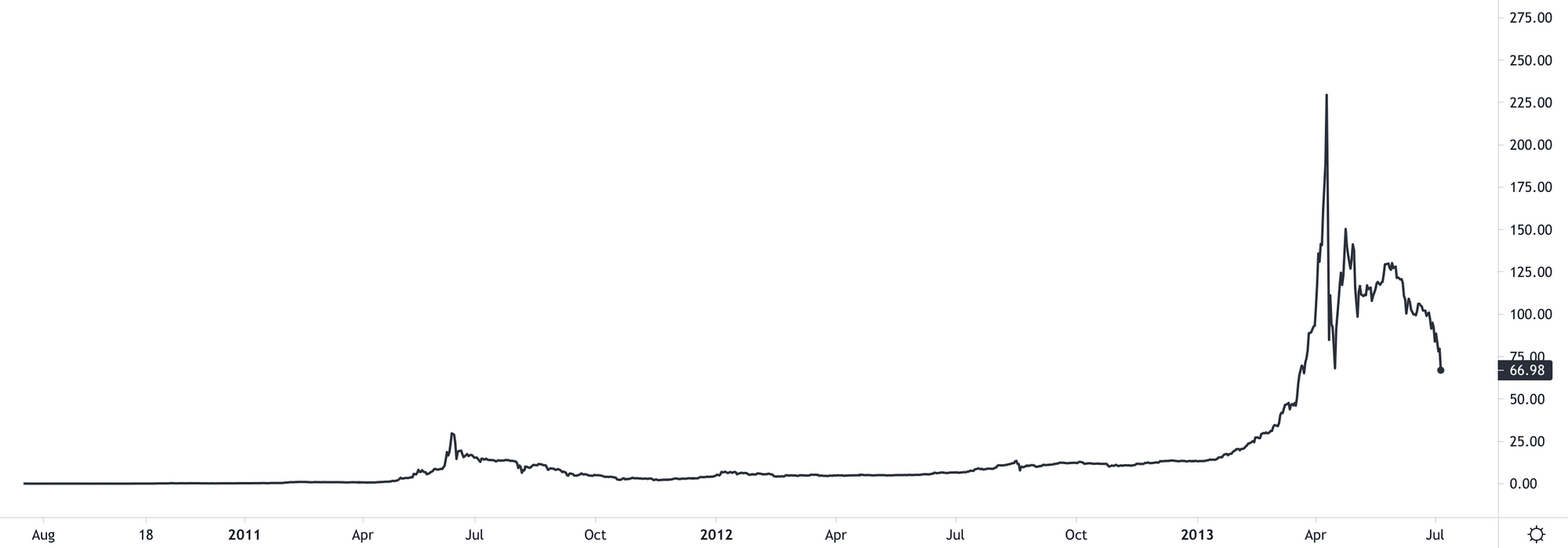
Je ziet op de kaart hierboven al een klein bultje in 2011, en inderdaad, die gaan we ook nog even bekijken. Bitcoin was toen zo nieuw dat er nog weinig overlijdensberichten in de kranten stonden.
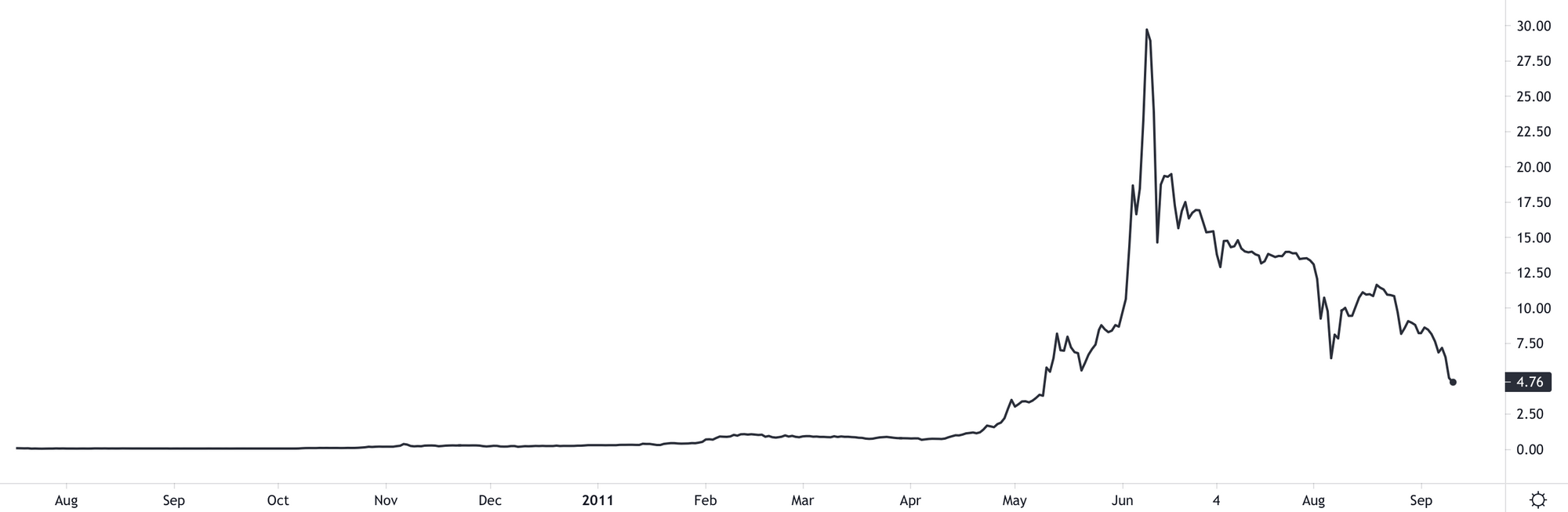
Dit is de reden dat we bitcoingrafieken vrijwel altijd op een logaritmische y-as tekenen. Daarbij is elk streepje een verdubbeling: 1, 2, 4, 8, 16, enzovoorts.
Dat is logisch bij ontwikkelingen die exponentieel van aard zijn, zoals de adoptie van een nieuwe technologie. Die volgt een logistische curve, dat is exponentiële groei waarbij de exponent steeds lager wordt door verzadiging. Net als bij de verspreiding van een virus waar uiteindelijk groepsimmuniteit ontstaat.
Het aantal bitcoiners groeit met verdubbelingen, en omdat het aanbod vastligt, stijgt de prijs ook met verdubbelingen. En bij exponentiële groei hoort een logaritmische y-as, zodat het resultaat een rechte lijn is. Hieronder zie je de bitcoinkaart met een logaritmische y-as, en daarin de vijf kaartjes van hierboven gemarkeerd.
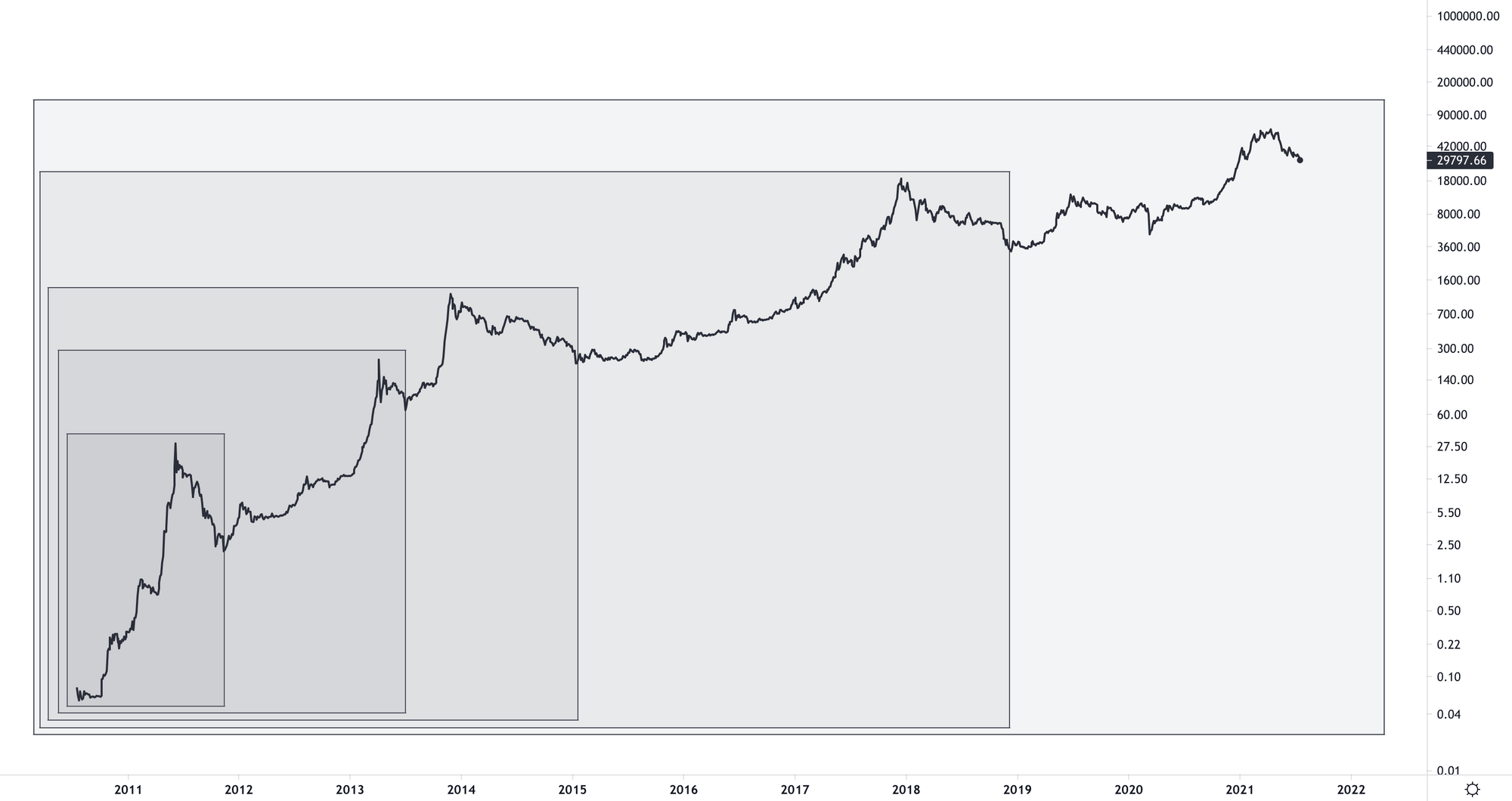
De koers volgt geen rechte lijn maar buigt steeds wat verder af. Dat betekent dat de verdubbelingen steeds iets langer duren. Uiteindelijk zal de koers afvlakken en stabiliseren op een niveau dat past bij volledige adoptie. Dan is een lineaire kaart wellicht beter. Maar dan zijn we nog wel een jaar of tien verder.
Dat wil zeggen: als bitcoin wereldwijde adoptie bereikt. Het kan natuurlijk altijd naar nul, namelijk als mensen hun interesse verliezen en afscheid nemen van bitcoin. Bijvoorbeeld omdat het wereldwijd verboden wordt of er een technisch probleem ontstaat dat niet op te lossen is. Vooralsnog is dat niet aan de hand en moeten we ons niet bang laten maken door angstwekkende lineaire grafieken!

